首页热点资讯详情

量化投资组合分散化的新视角——基于ENB探究经典投资组合模型的分散化效果

2024-07-24 15:26:17 来源：迈德瑞投资

关键字：量化投资投资组合

本期观点来自——迈德瑞投资

摘要：在构建投资组合时，“不要把所有的鸡蛋放在一个篮子里”是每一位投资者都遵循的重要原则之一。然而，如何准确衡量我的投资组合是否足够多元化？风险足够分散呢？本文将从Effective Number of Bets(ENB)这个独特的视角入手，探究等权重、保证金等权、收益预期加权、风险平价和均值方差五种经典投资组合模型在实际商品期货市场上的分散化效果。结果显示，均值方差模型在风险分散效果上表现最优，其ENB均值和中位数均显著高于其他模型。在持仓个数远少于其他模型的情况下，依然能实现高效的多元化。这表明均值方差模型在追求风险与收益最优化过程中，具有更优秀的“分散下注”效果。

一、引言

投资市场中存在多种不同类型的资产类别，如股票、债券、商品、房地产等。每种资产类别都有其独特的特征和表现方式，这使得它们在市场中的表现各不相同。每种资产类别之所以独特，是因为它们受到不同因素的影响。例如，债券的表现可能受到利率变动、国家政策、通货膨胀等多种因素的影响，而股票则更多地受到公司业绩、行业动态、宏观经济环境等多种因素的影响。尽管各资产类别有其独特性，但它们的回报在很大程度上也受一些共同因素的影响。这些共同因素可能包括经济增长、通货膨胀、利率水平等宏观经济指标，也可能是某一时期的特定宏观事件比如金融危机、战争、疫情等。

因此，在构建投资组合时，“不要把所有的鸡蛋放在一个篮子里”成为了每一位投资者遵循的重要原则之一。通过投资分散化，我们不仅能够降低单一资产或市场波动对整体投资组合的冲击，还能捕捉更多元化的投资机会，实现风险与收益的平衡。但什么是真正的有效分散？简单地将资金均匀分配到几只股票上，虽看似遵循了“不要把所有鸡蛋放在一个篮子里”的投资原则，却可能忽略了个股之间往往存在着难以察觉的紧密联系与共同风险暴露，即所谓的“系统性风险”。看起来不同的篮子，在市场风暴来临时，它们往往会同涨同跌。这意味着，仅仅依靠数量上的分散，可能并不能真正达到风险降低的目的。因此，评估我们投资组合的分散化水平是至关重要的，它关乎我们能否有效抵御风险并捕捉多元化的投资机会。

那么，如何准确衡量我的投资组合是否足够多元化？风险足够分散呢？

接下来，本文将从一个新颖的角度出发，对投资组合的分散化程度进行量化分析，并借助这一量化指标，深入探究经典投资组合模型在分散化方面的实际效果。

二、新视角 —— Effective Number of Bets

众多相关的文献研究中提出了各种不同的投资组合多样化衡量方法。比如基于资产权重的赫芬达尔指数(Herfindahl Index)：用投资组合中的资产权重平方总和来衡量投资组合的集中度。Choueifaty和Coignard(2008)提出了分散化指数(Diversification Ratio)：它利用资产组合中各资产的加权平均波动率与组合整体波动率的比值来量化组合的分散效果。虽然以上这些传统的分散化度量方法在评估投资组合多元化方面有其价值，但它们所揭示的信息仍然较为片面，未能全面且深入地反映投资组合中资产间的独立性和相互作用的复杂性。因此，探索一种能够更综合、更精准地衡量投资组合多样化程度的新方法，对于评价投资组合多元化和风险管理具有重要意义。

为了克服这些局限性，Meucci(2010)提出了Effective Number of Bets(以下简称“ENB”)这一概念。他基于PCA分析，从资产收益中提取出独立的因子，并使用因子暴露分布的熵（entropy）作为衡量指标，量化一个投资组合中真正隐含的、同等大小且互相独立的风险/回报(bets)来源数量。换句话说，ENB是通过考虑投资组合中各资产的风险贡献、资产间的相关性以及潜在的非线性影响，计算出的一个能够反映投资组合中有效独立风险/收益来源数量的指标。

当因子暴露分布较为均匀时，意味着投资组合中的不同因子对组合整体风险和收益的贡献相对均衡，没有哪一个因子能够单独主导投资组合的表现。此时ENB值通常较高，表示投资组合中包含了较多的有效独立风险/收益来源，风险得到了较好的分散。相反，如果因子暴露分布非常集中，即某个或某些因子占据绝大多数的暴露，那么投资组合的表现将高度依赖于这些少数几个因子。此时ENB值会较低，表示投资组合中的有效独立风险/收益来源数量较少，风险集中度较高。

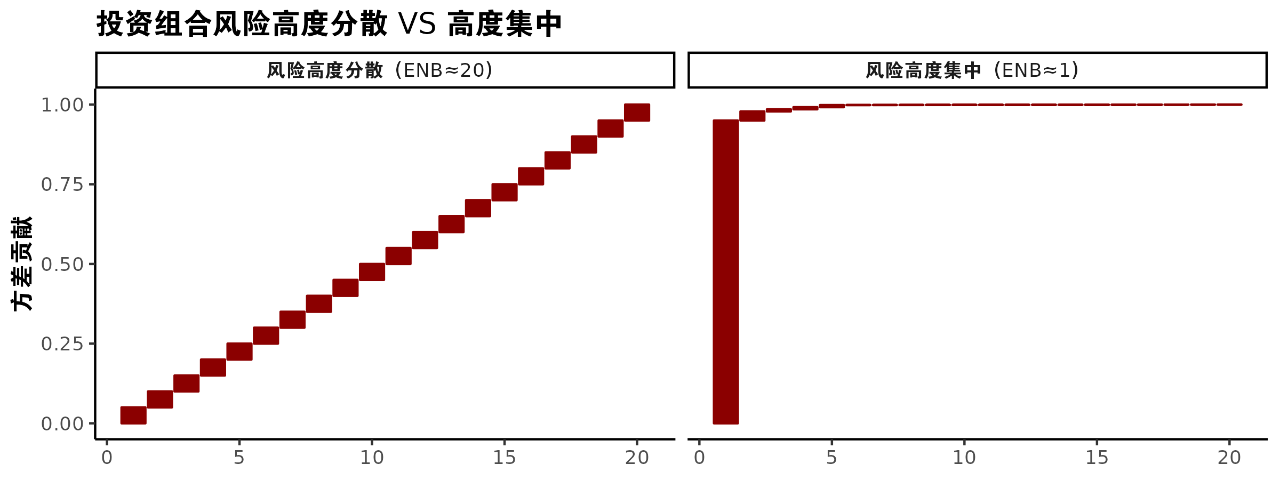
简单来说，ENB可以理解为投资组合中能够独立产生风险/收益的有效组成部分的数量。这个数量并非直接对应于投资组合中实际涵盖的风险因子数量，而是基于风险分散的视角，评估投资组合在多大程度上实现了“分散下注”于多个独立且差异化的风险因子上。对于具有N个资产的投资组合，ENB值介于1到N之间。如上图所示，左/右两边分别展示了投资组合风险高度分散/集中的情况，即ENB为最大值N或1的极端情况。

三、经典投资组合模型的分散化对比

基于上述ENB的重要性和应用价值，本文聚焦于国内期货市场，选取了2012-2023年期间符合严格筛选标准的41个高流动性期货品种作为研究对象。需要注意的是，研究样本并非从一开始就具备完整的41个期货品种，而是随着市场的不断发展和新品种的陆续推出，符合我们筛选条件（即高流动性）的期货品种数量逐渐增加，最终达到了我们所研究的41个品种。

为了探索不同投资组合模型在实际应用中的分散化效果，本文采用了等权重、保证金等权、收益预期加权、风险平价和均值方差五种常见且具有代表性的模型进行了回测分析。为贴近实际期货市场操作环境，我们在回测过程中设定了所有模型均允许做空，并采用了日频调仓策略。通过对比分析这五种模型在回测期间的ENB数量变化及其分布特征，我们可以深入了解不同模型在风险分散方面的表现差异。

下图直观展示了五种模型ENB数量随时间的演变趋势，其中，除均值方差模型外，其余四种模型在ENB数量的时间序列变化上展现出高度的相似性，而均值方差模型则表现出显著的不同。

结合下方的ENB分布图，可以进一步发现，等权重和收益预期加权模型在ENB的均值和中位数水平上均处于较低区间，表明这两种模型风险集中度较高。保证金等权模型相较于前二者，其在ENB均值和中位数上有所提升，风险平价模型则更高一筹。而均值方差模型则显著区别于其它模型，其ENB的均值和中位数均超过15。虽然风险平价模型在历史上也出现过ENB数量超过20的情况，但绝大部分的时间它的ENB水平都低于10；而均值方差模型大部分的时间ENB个数都在10-20这个区间。由此可以说明，从ENB的角度，均值方差在追求投资组合风险与收益最优化的过程中，“分散下注”的效果最好，且明显优于其它模型。

为了进一步探究各模型的分散化情况，我们统计了回测期间不同模型的持仓个数。下图展示了五种模型的持仓个数时序图，可以看到，均值方差由于模型本身的特殊性，并不会同时持有所有期货品种。而其他模型由于并不进行品种筛选，因此其持仓个数就等于可投资的合约种类数。相对于其他模型而言，均值方差天然有着选择性持仓的特点。

通过下方均值方差与其他模型在不同年份的持仓个数均值对比，我们发现均值方差在绝大部分时候，都只持仓了不到全部品种的一半。一方面这反映了均值方差模型自身的特性：寻求投资组合在预期收益与风险之间的最佳平衡，即识别出那些对组合整体风险贡献较小但预期收益相对较高的资产，从而给予它们更高的配置权重，而对于那些风险高或预期收益低的资产，则可能选择不纳入或少量纳入投资组合。另一方面，均值方差模型在持仓个数的选择上，实际上是在遵循一种效率原则：通过精心挑选一部分最具代表性的资产进行配置，可以在保持投资组合多样性和风险分散的同时，实现更高的投资效率。

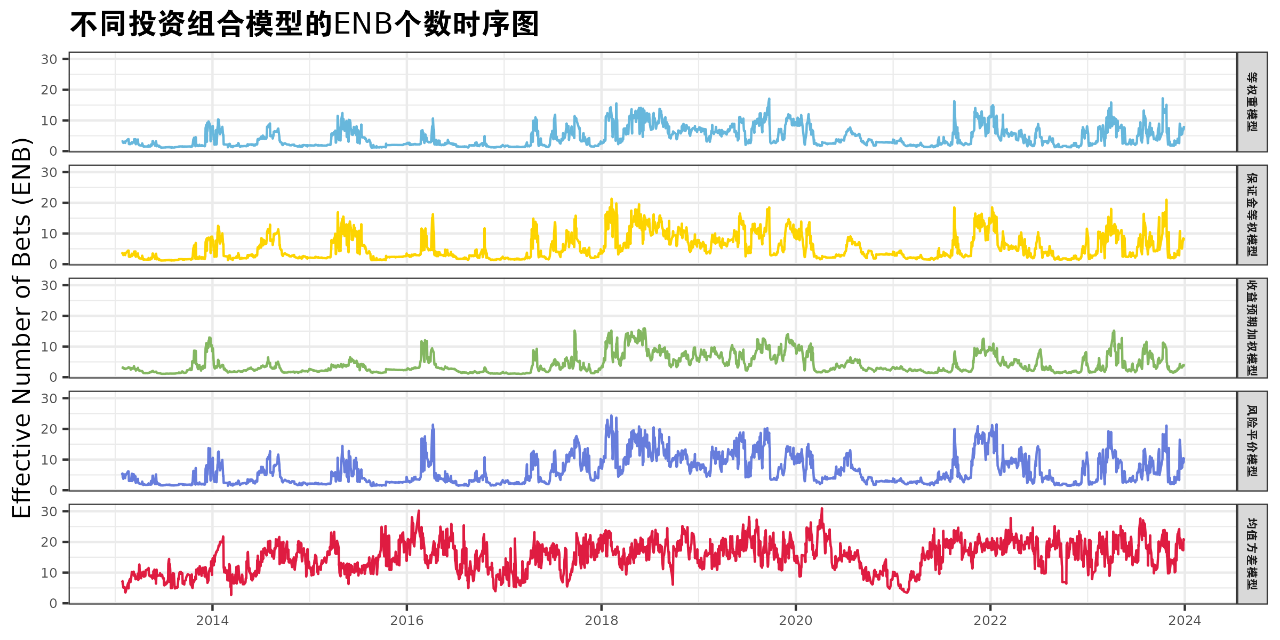
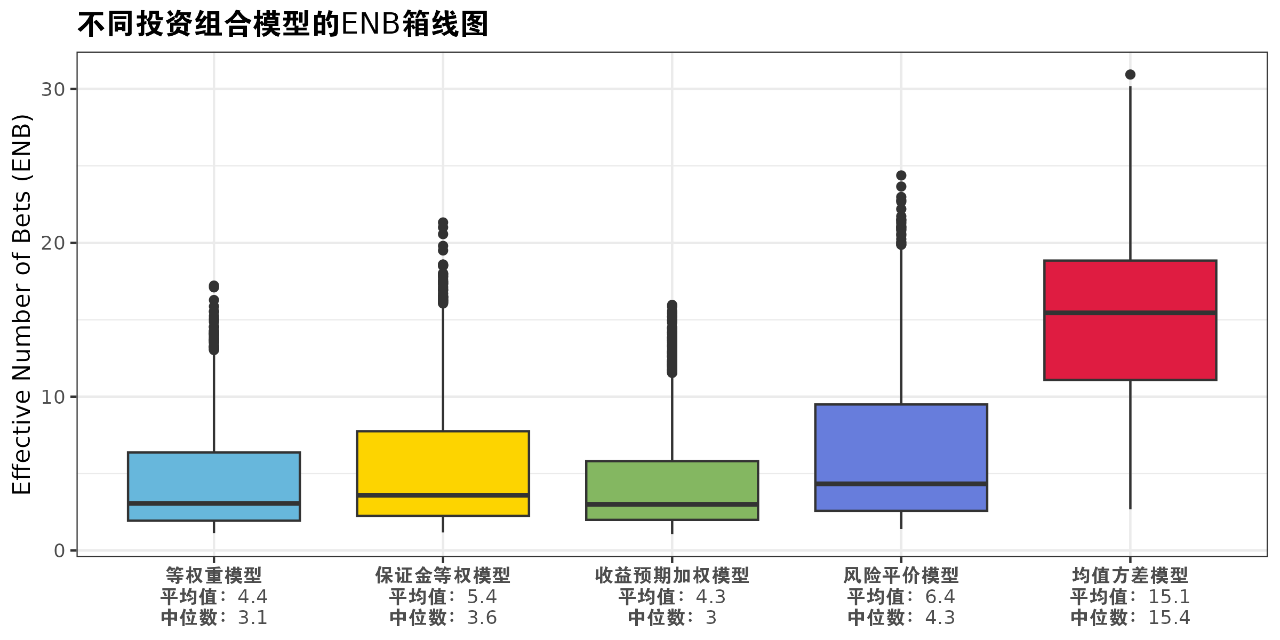
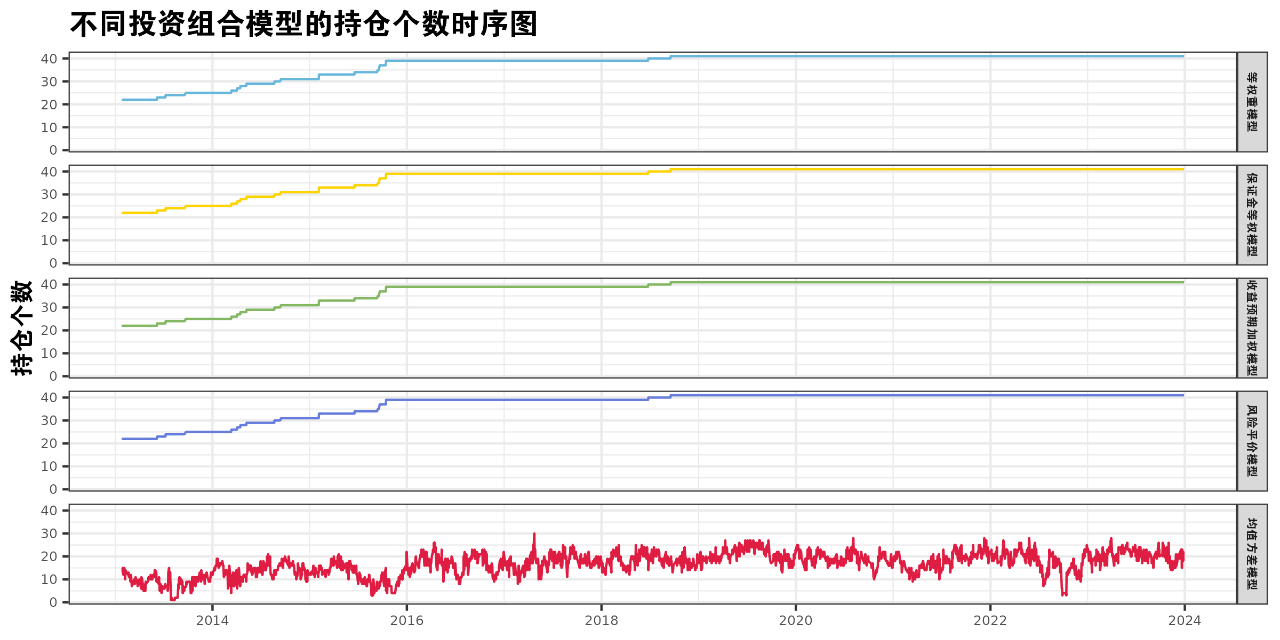
总结

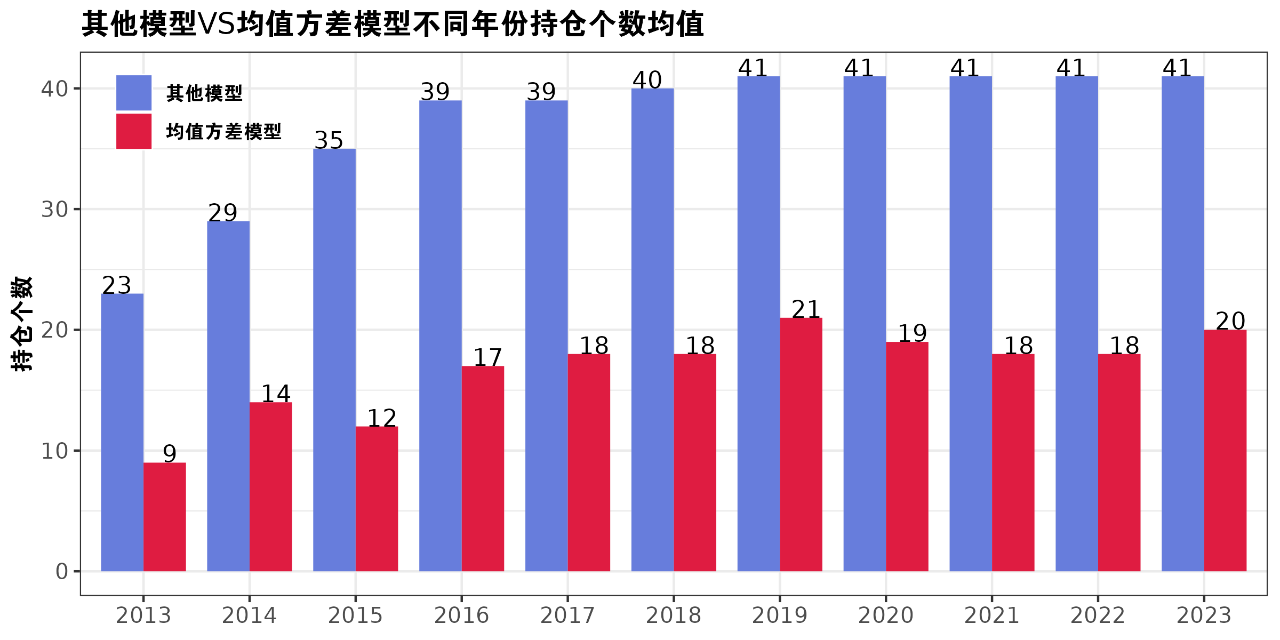
本文通过对比五种投资组合模型在国内商品期货市场的风险分散效果，发现均值方差模型展现出了相较于其他资产配置模型的显著优势。首先，它的ENB值（一个衡量风险集中度和多元化效果的指标）更高，这一结果直接反映了均值方差模型在构建投资组合时，能够更有效地分散风险，实现更低的风险集中度。这种优势主要得益于均值方差模型对资产间协方差的精确考量，以及它在预期收益与风险之间寻求最佳平衡的能力。

其次，尽管均值方差模型的持仓个数相对较少，但这并不妨碍其实现卓越的多元化效果。相反，这一特点恰恰体现了模型在资产配置上的高效性和精准性。仅仅通过配置少量的关键资产，就可以实现投资组合的多样性。

综上所述，ENB作为衡量投资组合分散化效果的新指标，为投资人开辟了全新的评估维度。基于风险分散的视角，均值方差在国内商品期货市场的应用中展现出了更优秀的“分散下注”效果，能真正有效地实现分散化投资。

免责声明：本文根据迈德瑞投资相关内容整理而成，我们的主要目的在于分享信息。若文章内容涉及投资建议，切勿直接作为投资依据。市场瞬息万变，投资请三思而后行。

责任编辑：Rachael

量化投资组合分散化的新视角——基于ENB探究经典投资组合模型的分散化效果

相关新闻

焦点新闻

与我们沟通